Python 3.3 is out. I use buildout.python to configure and make pythons on OS X.

(p33)krusty-2:p33 seang$ python
Python 3.3.0 (default, Sep 29 2012, 10:03:39)
[GCC 4.0.1 (Apple Inc. build 5493)] on darwin
Type "help", "copyright", "credits" or "license" for more  information.
>>>

I'm continuing to have fun with functional style Python map hacking. I've blogged about different aspects of this, but here's my first try at putting it all together: data access to map projection to folding everything down into a map image. After writing three functions operating on single feature records (one for drawing, one for projection, one for weighting by attributes), I can get a basic choropleth map of world population density in 4 lines of Python. I'll introduce those functions one at a time starting with feature drawing.

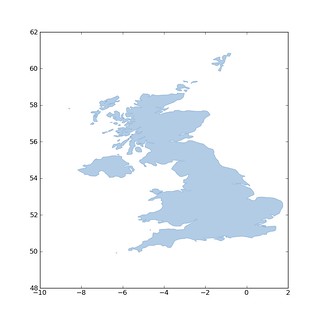
Next, feature projection using Pyproj (and PROJ4).

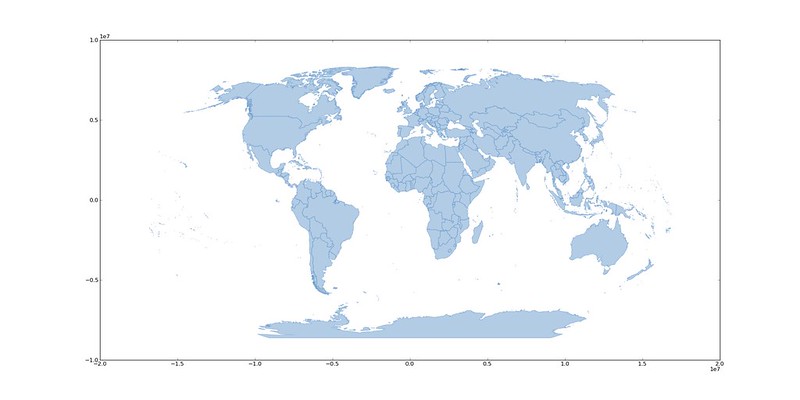
Finally, classification of features by their attributes.

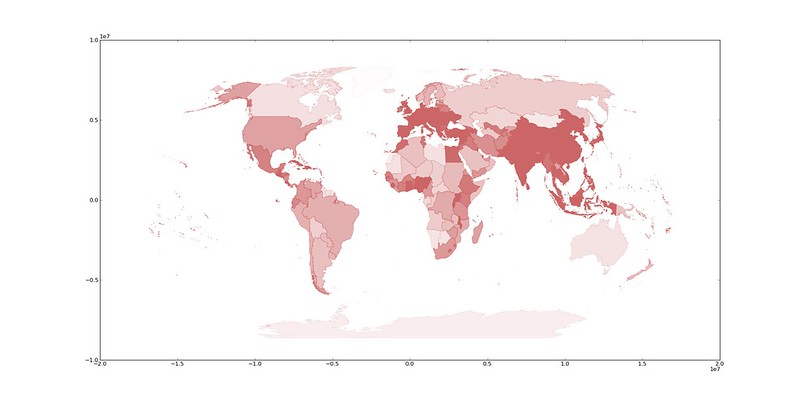
Code like zip(*func(*zip(*ring)) is probably taking it a little bit too far. While Python permits functional programming, its syntax isn't designed for readibility of functional code.

Update (2012-09-06): I've made 2 kinds of edits to the source in the gists. First, I've changed the drawing function so that it takes and returns a Matplotlib figure and noted why the function is impure. Mutability is essential to Matplotlib figures, there's no easy around this. The second bunch of edits restores as much referential transparency as I can: although the figures are mutable, they are only instantiated within the reduce expression and therefore can't be mutated by any other code.

It's been a while since I've used or written about Clojure, but I seized an opportunity to do so today. A Shapely user has been wondering what is up with simple, yet invalid polygons. The following WKT polygon:

"POLYGON ((0 0, 0 2, 2 2, 2 0, 0 0), (0 0, 0 1, 1 1, 1 0, 0 0))"

has a 2x2 square exterior ring and a square 1x1 interior ring that snaps precisely into its lower left quadrant.

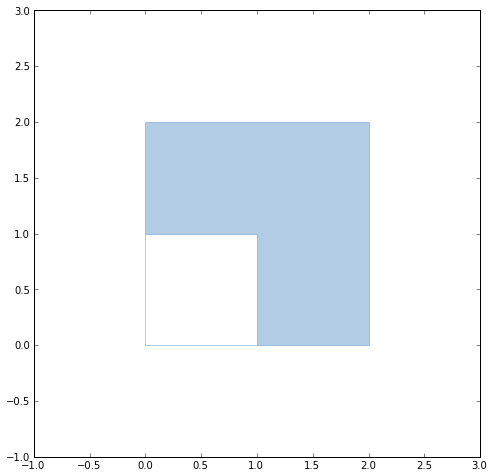
The interior ring is not a true "hole" because the rings overlap. In the simple features sense this is an invalid polygon, and Shapely (with GEOS 3.3.0) confirms it.

>>> ring1 = [(0, 0), (0, 2), (2, 2), (2, 0), (0, 0)]
>>> ring2 = [(0, 0), (1, 0), (1, 1), (0, 1), (0, 0)]
>>> from shapely.geometry import Polygon
>>> q = Polygon(ring1, [ring2])
>>> q.area
3.0
>>> q.is_valid
False

But what's this?

>>> q.is_simple
True

GEOS is a port of JTS – what would JTS do? I'm not a Java programmer, but there's Clojure: its REPL is a handy means of answering that question. I've got JTS and JTSIO 1.8.0 in my classpath here.

user=> (def wkt
    "POLYGON ((0 0, 0 2, 2 2, 2 0, 0 0), (0 0, 0 1, 1 1, 1 0, 0 0))")
#'user/wkt
user=> wkt
"POLYGON ((0 0, 0 2, 2 2, 2 0, 0 0), (0 0, 0 1, 1 1, 1 0, 0 0))"
user=> (def p (.read (com.vividsolutions.jts.io.WKTReader.) wkt))
#'user/p
user=> p
#<Polygon POLYGON ((0 0, 0 2, 2 2, 2 0, 0 0), (0 0, 0 1, 1 1, 1 0, 0 0))>
user=> (.getArea p)
3.0
user=> (.isValid p)
false
user=> (.isSimple p)
true

JTS, too, says it's simple. Maybe simple features simplicity isn't meaningful for polygons... and a check of the JTS source confirms this.

[isSimple()] Returns true, since by definition LinearRings are always simple.

I can see the rationale, but I think we'll consider breaking with JTS and GEOS on this one. It would be a first.

Update (2012-09-02)

In hindsight, the case above isn't such a good example. The rings themselves are simple. The polygon is only invalid because they overlap. Instead, here's the case of a bowtie polygon with a self-crossing exterior ring and no interior rings.

wkt = ("POLYGON (("
       "39.1451330299999967 23.7510081600000014, "
       "97.0537220899999937 40.5455008799999987, "
       "105.2652701399999984 48.1330221300000005, "
       "100.9175268500000016 58.4333681499999997, "
       "71.5608144800000048 83.5511480100000057, "
       "60.7118916800000008 86.2531609899999978, "
       "62.0046980799999972 75.1478175999999962, "
       "83.1631000699999987 42.8207167300000009, "
       "92.8230586199999976 37.1917558199999974, "
       "95.9940112900000031 26.4705124599999984, "
       "106.2205448200000006 15.5197519199999991, "
       "39.1451330299999967 23.7510081600000014"
       "))" )

bowtie = loads(wkt)
reduce(draw, [bowtie], gca())

Note that I'm exploiting Python's implicit line joining and string literal concatenation to give a little bit of structure to this geometry's WKT representation.

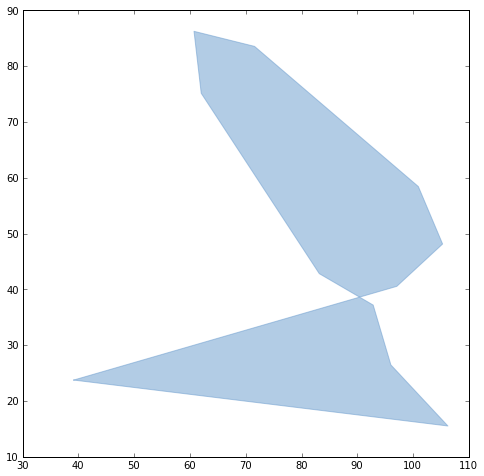
The test of simplicity is performed by GEOS, in which the exterior ring and polygon are simple by defintion.

print bowtie.is_valid
print bowtie.is_simple
print bowtie.exterior.is_simple

False
True
True

If we test the ring as though it were a line we get the opposite result.

from shapely.geometry import LineString
print LineString(bowtie.exterior).is_simple
# False

Whether rings should be simple by definition is, I feel, more a matter of taste than correctness. Letting rings report that they are in fact not simple is more to my taste. The simplicity of a polygon would then be the product of the simplicity of its rings.

from itertools import chain
print all(r.is_simple for r in chain([bowtie.exterior], bowtie.interiors))
# True

By the way, Python's all() short circuits in a good way: as soon as is_simple evaluates to False in the chain, it returns False.

This is very sad news. I use John's Matplotlib often and blogged about it just yesterday. His close friends have set up a memorial fund to help ensure the education of his children.

Update (2012-08-31): I'm watching his recent SciPy keynote (via Kurt Schwehr).

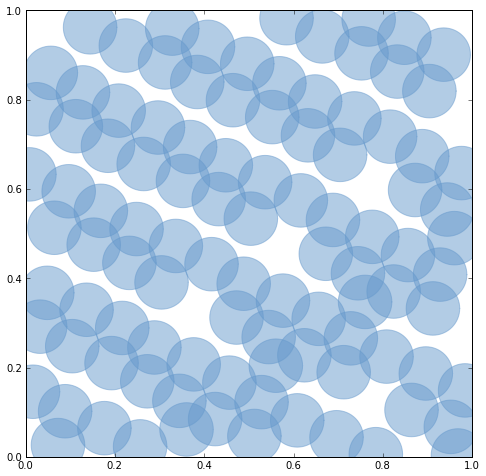
I've been using the IPython Notebook to plot geometric objects while writing new tests for Shapely.

$ ipython notebook --pylab inline

from functools import reduce
from itertools import islice
from descartes import PolygonPatch
from shapely.geometry import Point
from shapely.ops import unary_union

BLUE = '#6699cc'

def halton(base):
    """Returns an iterator over an infinite Halton sequence."""
    def value(index):
        result = 0.0
        f = 1.0/base
        i = index
        while i > 0:
            result += f * (i % base)
            i = i/base
            f = f/base
        return result
    i = 1
    while i > 0:
        yield value(i)
        i += 1

def draw(axes, item):
    """Given matplotlib axes and a geometric item, adds the item as a patch
    and returns the axes so that reduce() can accumulate more patches."""
    axes.add_patch(
        PolygonPatch(item, fc=BLUE, ec=BLUE, alpha=0.5, zorder=2))
    return axes

The islice function is handy: you give it a child's head and it tells you if you need to go buy insecticidal shampoo. Actually, it slices iterators, even infinite ones like the Halton sequences above. Halton sequences are pseudorandom and deterministic; I'm using them instead of better random number generators to make the Shapely tests repeatable.

# Zip together two 100-item sequences to make 100 pseudo-random points.
coords = zip(
    list(islice(halton(5), 20, 120)),
    list(islice(halton(7), 20, 120)) )

# Buffer the points to make overlapping patches.
patches = [Point(xy).buffer(0.06) for xy in coords]

# Note: with ipython's --pylab option, we've effectively imported
# all symbols from matplotlib's pylab module.
figsize(8, 8)

# Perform a left fold on the patches, applying the draw function (above)
# with the current axes as the accumulator. Aka "map rendering for hipsters."
reduce(draw, patches, gca())

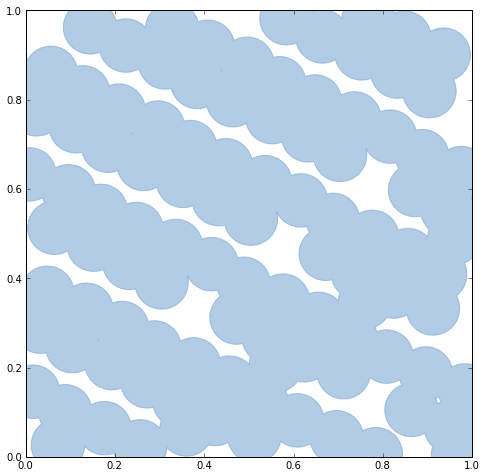
Shapely's unary_union function will replace the old cascaded_union function. It operates on any type of geometry, not just polygons.

# Dissolve continuously overlapping patches with the unary_union function.
u = unary_union(patches)
print u.geom_type
print u.area

# Output:
# MultiPolygon
# 0.87333863506

# A MultiPolygon is an iterator over its polygon parts, so we can perform
# a fold on it as well.
reduce(draw, u, gca())

The notebook file is here: https://gist.github.com/3503994.

Like its predecessor, unary_union currently requires a sequence of geometric objects. I'd love to allow iterators (lazy sequences) as well.

OGC Seeks Comments on GeoServices REST API Candidate Standard:

Using this API, clients, such as a web browser application, issue requests to resources on the server identified by structured Uniform Resource Locators (URLs). The server responds with map images, text-based location details or other representations of geospatial information. From a services perspective the API offers a mechanism to interact with map, image and feature services and perform geospatial analysis. This JavaScript Object Notation (JSON)-based, RESTful API is intended to make implementing servers instantly usable by developers working with widely used REST-based scripting and programming languages, as well as mobile platforms. End users can then use these developers' Web applications to discover and access the services and use them in their workflows.

Widely used REST-based scripting and programming languages? Really? As someone said to me last night, this is remarkable handwaving even for a standards organization. Has the meaning of REST diffused entirely into the void? My enthusiasm for reading the candidate standard is a little dampened, I must say, and it was soggy to begin with. This is all another reminder of how "Standards are Great, but Standardisation is a Really Bad Idea."

body_html_template

After a long dry spell, moisture has arrived from the tropics and the skies have been opening up. We got an inch Friday evening, an inch and a half Saturday evening, and an inch or so by 9:30 PM Sunday night with another 4 hours of light rain after that. The ditch behind my house overflowed and so did its parent, Spring Creek. My bike's bottom bracket is due some work anyway, so early this morning I peddled down the flooded trail to see what there was to see.

The cattails in the ditch add some greenery and structure to an otherwise ugly and weedy lot, and provide some nice habitat for red-winged blackbirds, but have mostly filled the channel and may have contributed a bit to the flooding here.

The pond on Spring Creek which had been disappearing was full again and the creek had flooded the bike path just west of the Centre Avenue underpass. On the dotted yellow line of the bike path, I came across this crayfish. It looked a bit battered, missing one pincer and one antenna.

I've updated the Shapely manual for 1.2.15 and finally added long overlooked documentation and illustrations (using matplotlib) for the parallel_offset method.

I'm a bit baffled by the gap in the right side offset. Is it intended or a numerical bug?

By the way, I'm surprised at the rate of downloads for this version. Exciting.

Shapely 1.2.5 is out: http://pypi.python.org/pypi/Shapely/1.2.15. This release is mostly concerned with helping packagers downstream. Changes:

• Eliminate numerical sensitivity in a method chaining test (Debian bug #663210).

• Account for cascaded union of random buffered test points being a polygon or multipolygon (Debian bug #666655).

• Use Cython to build speedups if it is installed.

• Avoid stumbling over SVN revision numbers in GEOS C API version strings.

There is a growing list of features in GEOS 3.3.x that Shapely isn't accessing yet and I'm looking forward to getting to these later this summer.