More IPython Notebook and Shapely
I've been using the IPython Notebook to plot geometric objects while writing new tests for Shapely.
from functools import reduce from itertools import islice from descartes import PolygonPatch from shapely.geometry import Point from shapely.ops import unary_union BLUE = '#6699cc' def halton(base): """Returns an iterator over an infinite Halton sequence.""" def value(index): result = 0.0 f = 1.0/base i = index while i > 0: result += f * (i % base) i = i/base f = f/base return result i = 1 while i > 0: yield value(i) i += 1 def draw(axes, item): """Given matplotlib axes and a geometric item, adds the item as a patch and returns the axes so that reduce() can accumulate more patches.""" axes.add_patch( PolygonPatch(item, fc=BLUE, ec=BLUE, alpha=0.5, zorder=2)) return axes
The islice function is handy: you give it a child's head and it tells you
if you need to go buy insecticidal shampoo. Actually, it slices iterators, even
infinite ones like the Halton sequences above. Halton sequences are
pseudorandom and deterministic; I'm using them instead of better random number
generators to make the Shapely tests repeatable.
# Zip together two 100-item sequences to make 100 pseudo-random points. coords = zip( list(islice(halton(5), 20, 120)), list(islice(halton(7), 20, 120)) ) # Buffer the points to make overlapping patches. patches = [Point(xy).buffer(0.06) for xy in coords] # Note: with ipython's --pylab option, we've effectively imported # all symbols from matplotlib's pylab module. figsize(8, 8) # Perform a left fold on the patches, applying the draw function (above) # with the current axes as the accumulator. Aka "map rendering for hipsters." reduce(draw, patches, gca())
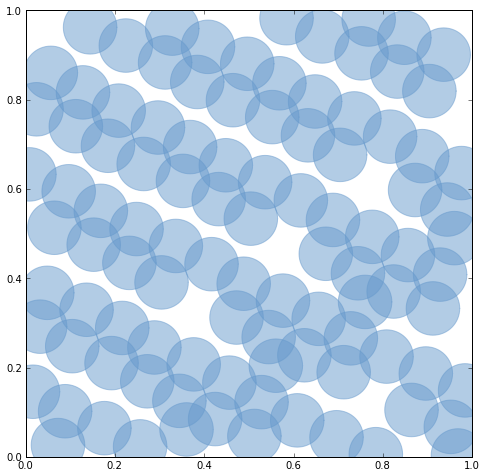
Shapely's unary_union function will replace the old cascaded_union
function. It operates on any type of geometry, not just polygons.
# Dissolve continuously overlapping patches with the unary_union function. u = unary_union(patches) print u.geom_type print u.area # Output: # MultiPolygon # 0.87333863506 # A MultiPolygon is an iterator over its polygon parts, so we can perform # a fold on it as well. reduce(draw, u, gca())
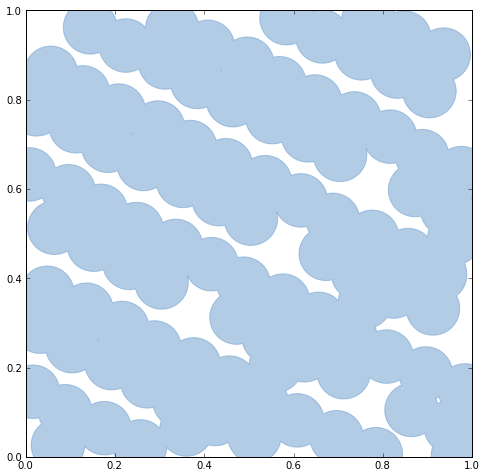
The notebook file is here: https://gist.github.com/3503994.
Like its predecessor, unary_union currently requires a sequence of geometric objects. I'd love to allow iterators (lazy sequences) as well.