Not as simple as it seems

It's been a while since I've used or written about Clojure, but I seized an opportunity to do so today. A Shapely user has been wondering what is up with simple, yet invalid polygons. The following WKT polygon:

"POLYGON ((0 0, 0 2, 2 2, 2 0, 0 0), (0 0, 0 1, 1 1, 1 0, 0 0))"

has a 2x2 square exterior ring and a square 1x1 interior ring that snaps precisely into its lower left quadrant.

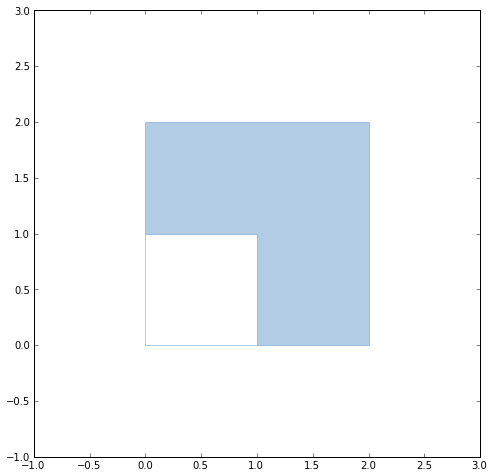
http://farm9.staticflickr.com/8457/7902097394_e74d2acc9e_o_d.png

The interior ring is not a true "hole" because the rings overlap. In the simple features sense this is an invalid polygon, and Shapely (with GEOS 3.3.0) confirms it.

>>> ring1 = [(0, 0), (0, 2), (2, 2), (2, 0), (0, 0)]
>>> ring2 = [(0, 0), (1, 0), (1, 1), (0, 1), (0, 0)]
>>> from shapely.geometry import Polygon
>>> q = Polygon(ring1, [ring2])
>>> q.area
3.0
>>> q.is_valid
False

But what's this?

>>> q.is_simple
True

GEOS is a port of JTS – what would JTS do? I'm not a Java programmer, but there's Clojure: its REPL is a handy means of answering that question. I've got JTS and JTSIO 1.8.0 in my classpath here.

user=> (def wkt
    "POLYGON ((0 0, 0 2, 2 2, 2 0, 0 0), (0 0, 0 1, 1 1, 1 0, 0 0))")
#'user/wkt
user=> wkt
"POLYGON ((0 0, 0 2, 2 2, 2 0, 0 0), (0 0, 0 1, 1 1, 1 0, 0 0))"
user=> (def p (.read (com.vividsolutions.jts.io.WKTReader.) wkt))
#'user/p
user=> p
#<Polygon POLYGON ((0 0, 0 2, 2 2, 2 0, 0 0), (0 0, 0 1, 1 1, 1 0, 0 0))>
user=> (.getArea p)
3.0
user=> (.isValid p)
false
user=> (.isSimple p)
true

JTS, too, says it's simple. Maybe simple features simplicity isn't meaningful for polygons... and a check of the JTS source confirms this.

[isSimple()] Returns true, since by definition LinearRings are always simple.

I can see the rationale, but I think we'll consider breaking with JTS and GEOS on this one. It would be a first.

Update (2012-09-02)

In hindsight, the case above isn't such a good example. The rings themselves are simple. The polygon is only invalid because they overlap. Instead, here's the case of a bowtie polygon with a self-crossing exterior ring and no interior rings.

wkt = ("POLYGON (("
       "39.1451330299999967 23.7510081600000014, "
       "97.0537220899999937 40.5455008799999987, "
       "105.2652701399999984 48.1330221300000005, "
       "100.9175268500000016 58.4333681499999997, "
       "71.5608144800000048 83.5511480100000057, "
       "60.7118916800000008 86.2531609899999978, "
       "62.0046980799999972 75.1478175999999962, "
       "83.1631000699999987 42.8207167300000009, "
       "92.8230586199999976 37.1917558199999974, "
       "95.9940112900000031 26.4705124599999984, "
       "106.2205448200000006 15.5197519199999991, "
       "39.1451330299999967 23.7510081600000014"
       "))" )

bowtie = loads(wkt)
reduce(draw, [bowtie], gca())

Note that I'm exploiting Python's implicit line joining and string literal concatenation to give a little bit of structure to this geometry's WKT representation.

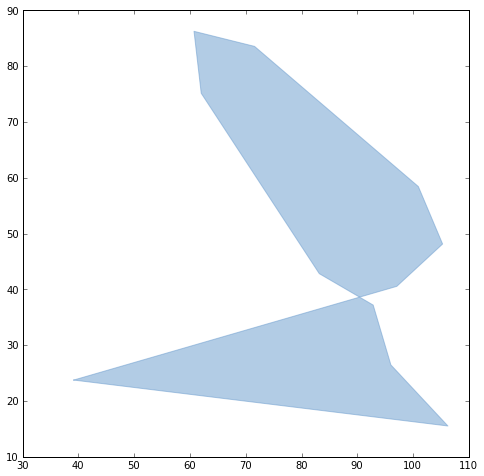
http://farm9.staticflickr.com/8440/7914978436_9e388d2c81_o_d.png

The test of simplicity is performed by GEOS, in which the exterior ring and polygon are simple by defintion.

print bowtie.is_valid
print bowtie.is_simple
print bowtie.exterior.is_simple

False
True
True

If we test the ring as though it were a line we get the opposite result.

from shapely.geometry import LineString
print LineString(bowtie.exterior).is_simple
# False

Whether rings should be simple by definition is, I feel, more a matter of taste than correctness. Letting rings report that they are in fact not simple is more to my taste. The simplicity of a polygon would then be the product of the simplicity of its rings.

from itertools import chain
print all(r.is_simple for r in chain([bowtie.exterior], bowtie.interiors))
# True

By the way, Python's all() short circuits in a good way: as soon as is_simple evaluates to False in the chain, it returns False.

Comments

Re: Not as simple as it seems

Author: Martin Davis

Sean, FWIW I agree with you that it makes more sense to have isSimple for polygons and rings report whether the underlying linework is simple. The current JTS hard-coded implementation was done for sake of expediency during the initial development of the library. It's a bit of a wasted opportunity to not allow isSimple to report self-intersecting linework (even if this still formally meets the SFS specification).

Semantics of isSimple for polygons?

Author: Martin Davis

This does raise the issue of what the semantics of isSimple for polygons should be. Should your original example of a hole overlapping the containing shell be reported as NOT simple? This would seem to be consistent with the OGC SFS definition of simplicity as "having no anomalous geometric points". But then isSimple pretty much becomes a synonym for isValid.

Or should it follow your idea of being the conjunction of the simplicity of the component rings?

It's not clear to me what the most useful semantics would be. It feels like the latter definition would be less redundant.

Re: Not as simple as it seems

Author: Sean

Thanks for the comments, Martin! Reading OGC 99-049, it seems my notion (above) of polygon simplicity is very naive. Non-simple surfaces would include things like cylinders and Möbius strips, right? Whereas you can represent (or misrepresent) a twisted, non- ring in our software (in WKT, WKB, or whatever), it's not possible to represent or misrepresent surfaces-with-boundaries as OGC Polygons. In other words, it seems we can't even begin to describe a valid, non-simple surface using the strings "polygon" or "multipolygon".

Re: Not as simple as it seems

Author: Martin Davis

That definitely seems like a deeper notion of simplicity. But as you say, not something that can be represented in the 2D world of the SFS.

Really it all comes down to what is most useful for people using the SFS. My original take was that simplicity was really only of interest in the case of linestrings, so I didn't worry too much about the case of polygons. (And it's still not clear to me that there's really a use case there...)