The fading shape of alpha

Surely you've seen the Flickr shapefiles public dataset and read Aaron Straup Cope's The Shape of Alpha about the why and the how of making those shapes. For some time I've been thinking that we could apply this kind of analysis to get a sense of the shape of fuzzy Pleiades places like the Mare Erythraeum, the territory of the Volcae Arecomici, or even Ptolemy's world. Not precise boundaries, which are problematic in many ways, but shapes that permit reasonably accurate queries for places bordering on the Volcae Arecomici or west of the Mare Erythraeum.

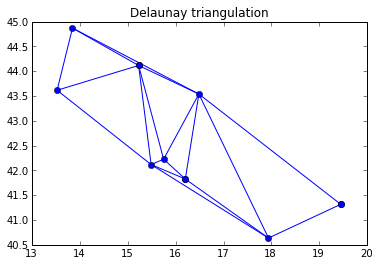
The Mare Adriaticum is our current test bed in Pleiades. We've made 9 different connections to it from precisely located islands, ports, and promontories. These play the part of the tagged photos in the Flickr story, and here they are as a GeoJSON feature collection: https://gist.github.com/3886076#file_mare_adriaticum_connections.json. My alpha shape analysis begins with a Delaunay triangulation of the space between these points. I used scipy.spatial.Delaunay to do it and benefited from the examples in this Stack Overflow post: http://stackoverflow.com/questions/6537657/python-scipy-delaunay-plotting-point-cloud.

import json
import numpy as np
from scipy.spatial import Delaunay

# JSON data from the gist above.
coordinates = [f['geometry']['coordinates'] for f in json.loads(data)]
points = np.array(coordinates)
tri = Delaunay(np.array(points))

# Rest as in SO post above.
...

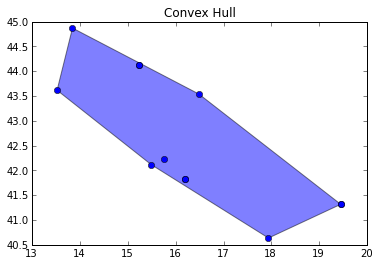
The nodes and lines of this triangulation are shown to the left below. Dissolving them yields the convex hull of the points, a figure that is slightly too big for Pleiades: points we want to have on the boundary of the Adriatic Sea, Iader to the north and the tip of the Gargano Promontory to the sourth, fall inside the hull. By what criteria might we toss out the peripheral triangles of which they are nodes and obtain an alpha shape more representative of the Adriatic? Printing out the radii of each triangle's circumcircle gives us this list:

0.916234205371
21.0145482369
1.85517410861
1.79158041604
0.887999941617
0.983745009567
1.2507779965
1.01471746864
0.430582735954
6.79200819757

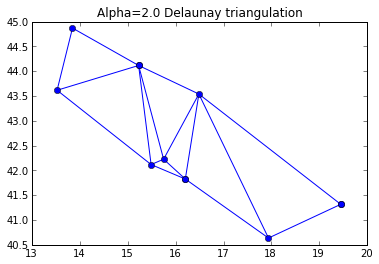
All of these are radii on the order of 1 except for 2 outliers. Those outliers are the narrow triangles we want to exclude from our hull. Setting a radius limit of 2 (α=0.5) via the code below removes the outlier triangles.

import math

edges = set()
edge_points = []
alpha = 0.5

# loop over triangles:
# ia, ib, ic = indices of corner points of the triangle
for ia, ib, ic in tri.vertices:
    pa = points[ia]
    pb = points[ib]
    pc = points[ic]

    # Lengths of sides of triangle
    a = math.sqrt((pa[0]-pb[0])**2 + (pa[1]-pb[1])**2)
    b = math.sqrt((pb[0]-pc[0])**2 + (pb[1]-pc[1])**2)
    c = math.sqrt((pc[0]-pa[0])**2 + (pc[1]-pa[1])**2)

    # Semiperimeter of triangle
    s = (a + b + c)/2.0

    # Area of triangle by Heron's formula
    area = math.sqrt(s*(s-a)*(s-b)*(s-c))

    circum_r = a*b*c/(4.0*area)

    # Here's the radius filter.
    if circum_r < 1.0/alpha:
        add_edge(ia, ib)
        add_edge(ib, ic)
        add_edge(ic, ia)

lines = LineCollection(edge_points)
plt.figure()
plt.title('Alpha=2.0 Delaunay triangulation')
plt.gca().add_collection(lines)
plt.plot(points[:,0], points[:,1], 'o', hold=1)

I dissolved the triangles using Shapely and render the hull using PolygonPatch from descartes.

from descartes import PolygonPatch
from shapely.geometry import MultiLineString
from shapely.ops import cascaded_union, polygonize

m = MultiLineString(edge_points)
triangles = list(polygonize(m))

plt.figure()
plt.title("Alpha=2.0 Hull")
plt.gca().add_patch(PolygonPatch(cascaded_union(triangles), alpha=0.5))
plt.gca().autoscale(tight=False)
plt.plot(points[:,0], points[:,1], 'o', hold=1)
plt.show()

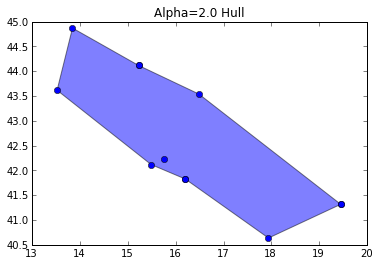
Can you see the difference? The hull pulls down a bit on the north edge and bumps up a bit on the south edge. It may not look like much to you, but now we're rescuing the Gargano Massif from the Adriatic – a fascinating place with unique geologic formations and 3 species of native giant hamsters. Who knows how many or how large these may have been in ancient times? (Update 2012-10-15: It's unlikely that Romans encountered the giant hamsters and hedgehogs of Pliocene Gargano.)

I've put a lot of work into making Shapely play well with Numpy and Matplotlib through the Python geospatial data protocol; it's fun to experiment with them like this. That interface also makes publishing a web map of my alpha shape trivial. The shape is exported to GeoJSON with a few lines of Python

from shapely.geometry import mapping

hull_layer = dict(
    type='FeatureCollection',
    features=[dict(
        type='Feature',
        id='1',
        title='Hull (Alpha=2.0)',
        description='See http://sgillies.net/blog/1154/the-fading-shape-of-alpha',
        geometry=mapping(cascaded_union(triangles)) )])

print json.dumps(hull_layer, indent=2)

and copied to a script in http://sgillies.github.com/mare-adriaticum to be used with Leaflet. Leaflet! If the new OpenLayers is designed around first-class treatment for GeoJSON we may yet return, but for now it's all Leaflet all the time in Pleiades.

I've run out of time today for playing with and writing about ancient alpha shapes, but have list of next things to do. It's obvious that I should be using the Web Mercator projection at least and probably an equal area projection when computing the circumcircles and triangulation and also obvious that there's no globally ideal alpha value. A statistical analysis of the circumcircle radii for each shape is certainly the right way to determine the outliers, and there may be different kinds of distributions involved. Meanwhile, this alpha shape of the Adriatic gets better as we anchor it to more precisely located places. A few more at the north end and the resulting shape has bounding box and centroid properties not much different than what you might come up with from an Adriatic Sea shape derived from a world coastlines dataset.

Enumeration of the problems I see in asserting fine boundaries for unmeasurable or intrinsically fuzzy places is another TODO item.

(With apologies to Aaron Straup Cope for the title of this post.)