Connecting places

The poster I made for DH 2011 shows "connects with" type relationships between several places, a new and distinctly "un-GIS" feature of Pleiades. It's meant to relate fuzzy places to each other with just enough semantics to afford researchers some useful and thought provoking networks, while not ruling out more specific future relationships.

Consider the figure below, a graph in which every node is a Pleiades place and every edge is a "connects with" relationship taken from the NeoGeo Spatial Ontology. This ontology is based on the Region connection calculus or RCC.

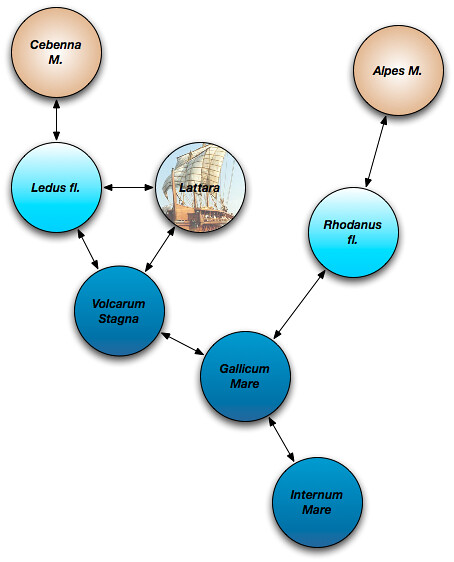
The Internum and Gallicum Mares are respectively the Mediterranean Sea and Gulf of Lion. Have you ever seen either of these bodies of water represented as a GIS feature? I have not. Typically, they manifest (or don't) on a map as negative space, labeled but border-less lacunae. Even when there's bathymetry on a map, the label is disconnected. If there's a feature dataset that allows one to answer the question "is the Mediterranean connected with the Gulf of Lion", I haven't seen it. Frontal boundaries do exist in the ocean, but they are dynamic features. Any dataset that modeled the boundary between the two as anything like national borders or real property lines would be more "truthy" than truthful. Still, geographers can agree that certain features define these bodies of water and that they are connected. The physical state of one affects the other on human time scales. People, goods, and information can travel by boat between these bodies of water, passing from one to the other, even if the exact moment and location of the transition is not determinable.

The Volcarum Stagna are the coastal lagoons (étangs) of the Languedoc. They are separated from the Gulf of Lion by narrow sand beaches. GIS analysis would say that the shorelines of the lagoons and gulf do not touch, but whether by canals or portage, the Volcarum Stagna and the Gulf of Lion are certainly connected from a transport perspective. Physically, too, as water is exchanged through the porous strips of intervening sand, themselves pushed around by the tides and waves of the sea.

The Ledus (now Lez) River heads in the foothills of the Cebenna Mons (Cévennes Mountains) and flows into the Volcarum Stagna at the ancient trading port of Lattara. It is connected with all three of those places. Likewise, the Rhodanus (Rhône) is connected with the Alps and the Gallicum Mare even though we're not able to say exactly what are the boundaries of the Alps, what is the exact course (and width) of the river, or what was the exact position of the mouth of the Rhône in ancient times.

GIS analysis can be quite sensitive to scale. The lengths of coastlines from 1:25000 and 1:1000000 (for example) scale datasets will differ unless the later is created by very careful generalization of the former. Now add computational geometry to the mix: connections found between features at a small scale may be different in number from those found between features at a large scale. Rather than twist lines and polygons beyond the limits of certainty and relevance to make them snap and connect and then require users to master complex GIS tools to derive relationships between places than might turn out to vary with scale, we can simply encode the most immediate relationships – at human scale – directly in the structured data about the places. The evidence for the relationships could very well be from GIS analysis, but it may also be from a reading of ancient or medieval maps, geographies, milestones, itineraries, manifests, or diaries.

The Ordnance Survey is a leader in publishing this kind of linked geographic data. See for example the resource about the City of Southampton, in which contained, containing, and touching cities, wards and boroughs are plainly enumerated. Some of the relationships don't follow from mathematical treatment; places might be part of other administrative regions from which they are geometrically disjoint. This is more or less what we're trying to do with Pleiades and it's been comforting to follow in the footsteps of OS researchers like John Goodwin. A difference in the Pleiades approach is that we're going to see how far we can get with no semantics other than "connects with", glossing over the difference between overlapping, touching, and the other RCC relations. Users tell me that our approach will be good enough for qualitative studies of trade and exchange in the ancient world.

Without a "disjoint from" relation, the Pleiades approach is akin to Facebook's. Absence of "dislike" semantics doesn't seem to be hurting the Facebook social graph, and I'm optimistic about the mileage Pleiades can get without implementing a "disjoint from" relation.